Asymptote
An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below:
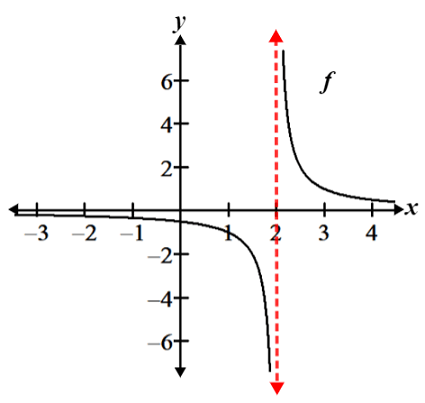
The asymptote is indicated by the vertical dotted red line, and is referred to as a vertical asymptote.
Types of asymptotes
There are three types of linear asymptotes.
Vertical asymptote
A function f has a vertical asymptote at some constant a if the function approaches infinity or negative infinity as x approaches a, or:
Referencing the graph below, there is a vertical asymptote at x = 2 since the graph approaches either positive or negative infinity as x approaches 2.

Horizontal asymptote
A function f has a horizontal asymptote at some constant a if the function approaches a as x approaches negative or positive infinity, or:
In the figure below, f(x) approaches y = 2 as x approaches either negative or positive infinity, so y = 2 is a horizontal asymptote.
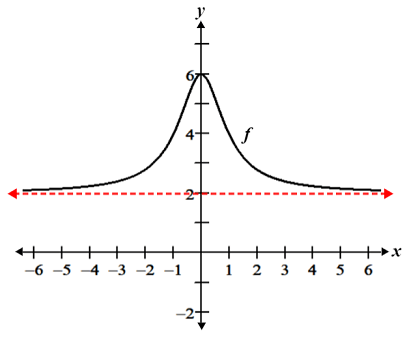
In certain cases, it is possible for the graph of a function to intersect its horizontal asymptote, as shown in the figure below:
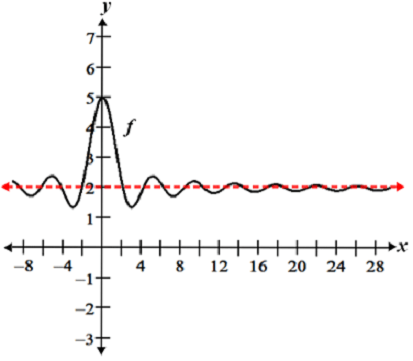
Furthermore, the graph of a function may have multiple horizontal and vertical asymptotes:
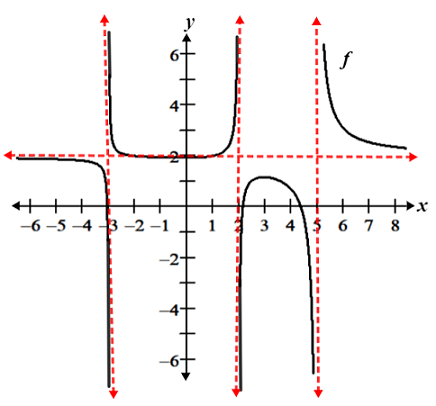
Referencing the figure above, f(x) has vertical asymptotes at x = -3, x = 2, and x = 5; it has a horizontal asymptote at y = 2.
Oblique asymptote
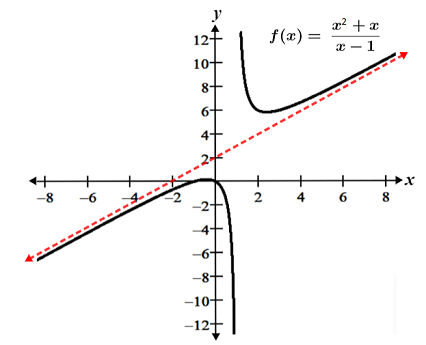
A function f has an oblique (slant) asymptote if it approaches a line of the form y = mx + b (where m ≠ 0) as x approaches negative or positive infinity. The graph of is shown in the figure below. It has an oblique asymptote at y = x - 1.
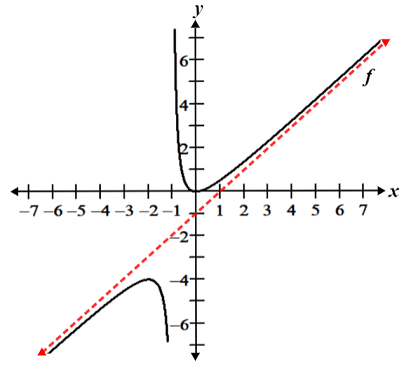
How to find the asymptotes of a rational function
A rational function is a function that can be written in the form . The techniques below apply to rational functions in which P(x) and Q(x) are polynomial functions and Q(x) ≠ 0.
Vertical asymptotes
To find the vertical asymptotes of a rational function f of the form described above, first find the points at which f(x) is undefined; these occur at the zeros of Q(x). Then:
- If P(x) and Q(x) have no common factors, f(x) has vertical asymptotes at the zeros of Q(x).
- If P(x) and Q(x) share common factors, holes in f(x) occur at the zeros of any shared factors, and f(x) has vertical asymptote(s) at the remaining zeros of Q(x).
Examples
Find any vertical asymptotes for the following functions:
i. The zeros of Q(x) occur when (x - 2) = 0 and (x + 3) = 0, so x = 2 and x = -3. Since there are no shared factors with P(x), f(x) has vertical asymptotes at x = 2 and x = -3, since these values of x result in f(x) being undefined. The graph of f(x) is shown in the figure below:
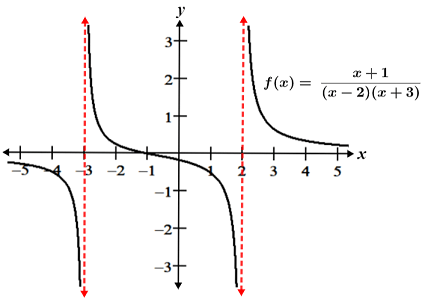
ii. Q(x) factors to (x + 2)(x - 2), so the zeros occur at x = ± 2, and f(x) is undefined at x = ±2. Since P(x) and Q(x) share the factor (x - 2), f(x) can be simplified as follows:
Thus, f(x) has a hole at x = 2, and a vertical asymptote at x = -2, as shown in the figure below.
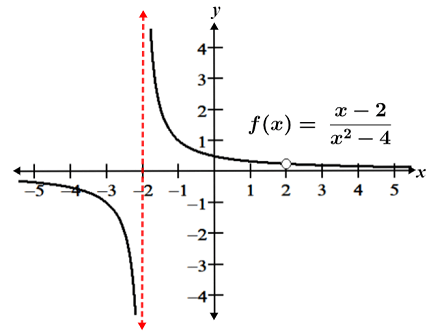
Horizontal asymptotes
To find a horizontal asymptote for a rational function of the form , where P(x) and Q(x) are polynomial functions and Q(x) ≠ 0, first determine the degree of P(x) and Q(x). Then:
- If the degree of Q(x) is greater than the degree of P(x), f(x) has a horizontal asymptote at y = 0.
- If the degree of P(x) is equal to that of Q(x), f(x) has a horizontal asymptote that is the ratio of the coefficients of the highest degree term of P(x) to that of Q(x).
- If the degree of P(x) is greater than the degree of Q(x), f(x) has no horizontal asymptote, though it may have a slant asymptote.
Examples
Find any horizontal asymptotes for the following functions:
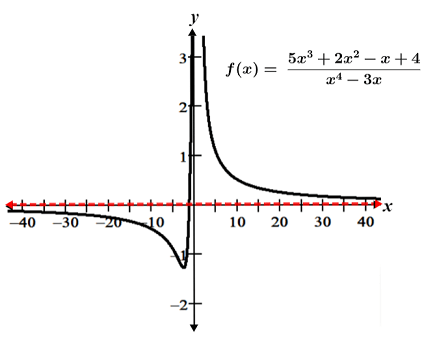
i. The degree of Q(x) is 4, since the highest order term of q(x) is x4. Similarly, the degree of P(x) is 3. Since Q(x) > P(x), f(x) has a horizontal asymptote at y = 0, as shown in the figure below.
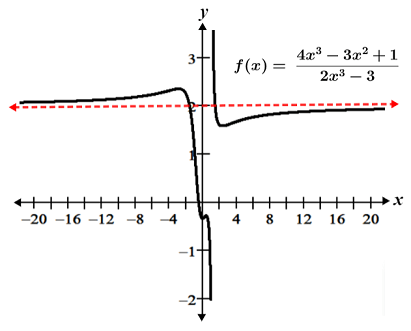
ii. The degree of both P(x) and Q(x) are 3. The corresponding terms are 4x3 and 2x3, respectively, and their coefficients are 4 and 2. Thus, f(x) has a horizontal asymptote at y = 4/2 = 2, as shown in the figure below:
Oblique asymptotes
To find an oblique asymptote for a rational function of the form , where P(x) and Q(x) are polynomial functions and Q(x) ≠ 0, first determine the degree of P(x) and Q(x). Then:
- If the degree of P(x) is exactly one greater than the degree of Q(x), f(x) has an oblique asymptote.
- The oblique asymptote can be found by dividing Q(x) into P(x). Given that s is the resulting quotient, f(x) has an oblique asymptote at y = s.
- Otherwise, f(x) does not have an oblique asymptote.
Example
Find any slant asymptotes for
Since the degree of P(x) is exactly one greater than Q(x), f(x) has an oblique asymptote, and we divide Q(x) into P(x):
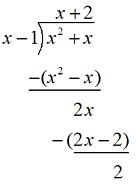
The quotient is s = x + 2, so f(x) has an oblique asymptote at y = x + 2, as shown in the figure below: