Function

A function is a relation between two sets in which each member of the first set is paired with one, and only one, member of the second set.

A function rule is a rule that explains the relationship between two sets.

Example

Two of the ways that functions may be shown are by using mapping (left) and tables (right), shown below.

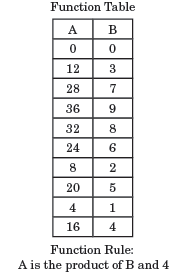Functions are also represented algebraically through expressions or equations. These expressions and equations describe the relationship between an independent and a dependent variable.

Example

3x + 4    f(x) = x

Functions can also be drawn as graphs. When represented as graphs, the dependent variable of the function is plotted on the y-axis while the independent variable is plotted on the x-axis. For discrete functions, each point of the function (x,y) is plotted as a coordinate. For non-discrete functions, those points are connected as a line.

Example

On a graph, the vertical line test can be used to determine whether or not a curve is a function. There is also the horizontal line test, which determines whether or not a funcntion is one-to-one. A one-to-one function is defined as a function in which distinct elements of its domain are never mapped to the same element of its co-domain, as shown below:

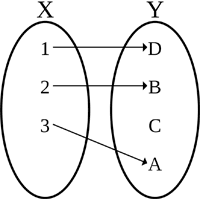
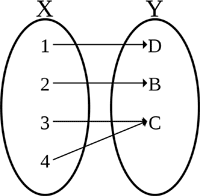
On the left is a one-to-one function, also known as an injective function. No X element is mapped to the same Y element. In contrast, the function on the right is a function that is not one-to-one, since two of the X elements, 3 and 4, are mapped to the same Y element, C.