Intersection
In set theory, the intersection of a collection of sets is the set that contains their shared elements. Given two sets, A = {2, 3, 4, 7, 10} and B = {1, 3, 5, 7, 9}, their intersection is as follows:
A ∩ B = {3, 7}
The intersection of two sets is commonly represented using a Venn diagram. In a Venn diagram, a set is represented by a circle. The intersection of sets A and B in the Venn diagram below is the shaded region where the two circles overlap.
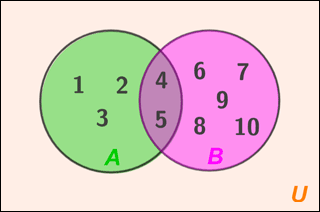
A = {1, 2, 3, 4, 5,} and B = {4, 5, 6, 7, 8, 9, 10}, so A ∩ B = {4, 5}. Note that A and B are part of 𝕌, the universal set (represented by the rectangle), which contains other elements that are not part of A or B.
Properties of intersections
Like other basic operations such as addition, set operations like intersections also have certain properties. Refer to the set page if necessary for a table of symbols commonly used in set theory.
Intersections and subsets
If set A is a subset of set B, then the intersection of the two sets is equal to set A. Using set notation:
if A ⊆ B, then A ∩ B = A
For example, if A = {4, 5, 6} and B = {4, 5, 6, 7, 8}, their intersection is {4, 5, 6}, or A.
Commutative law
The commutative law states that the order in which the intersection of two sets is taken does not matter. Given two sets, A and B:
A ∩ B = B ∩ A
Let A = {1, 2, 3} and B = {3, 5, 7}. The only common element the two sets have is 3. Thus, A ∩ B = B ∩ A = {3}. It doesn't matter whether we consider A or B first, the result will be the same.
Associative law
The associative law states that rearranging the parentheses in an intersection of sets does not change the result. Given sets A, B, and C:
(A ∩ B) ∩ C = A ∩ (B ∩ C)
The position of the parentheses doesn't matter since the intersection operation does not change the relationship between the sets. Comparing sets A and B first, then B and C, or B and C first, then A and B, doesn't change the relationship between A and B or B and C.
Distributive law
For sets A, B, and C, the distributive law states
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
where A is distributed to B and C. This is similar to the distributive property of multiplication in which multiplication distributes over addition. The Venn diagram below demonstrates the first law listed above:
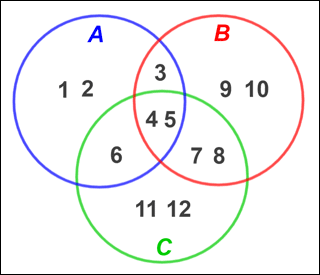
From the figure, A = {1, 2, 3, 4, 5, 6}, B = {3, 4, 5, 7, 8, 9, 10}, and C = {4, 5, 6, 7, 8, 11, 12}. Thus:
B ∩ C = {4, 5, 7, 8}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 11, 12}
The left side of the equation is:
| A ∪ (B ∩ C) | = | {1, 2, 3, 4, 6, 6} ∪ {4, 5, 7, 8} |
| = | {1, 2, 3, 4, 5, 6, 7, 8} |
The right side of the equation is:
| (A ∪ B) ∩ (A ∪ C) | = | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {1, 2, 3, 4, 5, 6, 7, 8, 11, 12} |
| = | {1, 2, 3, 4, 5, 6, 7, 8} |
The left and right sides are equal, confirming the distributive law.
De Morgan's laws
In set theory, De Morgan's laws are a set of rules that relate the union and intersection of sets through their complements.
Intersection of sets:
The complement of the intersection of two sets is equal to the union of their complements:
A ∩ B = AC ∪ BC
Given that A and B are subsets of the universal set 𝕌, this relationship can be seen in the figure below:

The intersection of A and B, A ∩ B, is shaded in red. Its complement, (A ∩ B)C is shaded in grey. The union of the complements of A and B, AC ∪ BC, is also shaded in grey.
Union of sets:
The complement of the union of two sets is equal to the intersection of their complements:
(A ∪ B)C = AC ∩ BC
Given that A and B are subsets of the universal set 𝕌, this relationship can be seen in the figure below:

The union of A and B, A ∪ B, is shaded in blue. Its complement, (A ∪ B)C is shaded in yellow. The intersection of the complements of A and B, AC ∩ BC is also shaded in yellow.
