Origin
The origin is a point where something begins or emanates from. In mathematics, the origin usually refers to a point on a number line or in a coordinate system.
Number lines
On a number line, the origin is at position zero, as shown below:

Each point on a number line corresponds to a real number and their positions relative to the origin. Numbers to the right of the origin are positive and numbers to the left of the origin are negative.
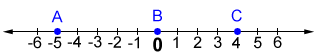
Point A is 5 left of the origin, point B is at the origin, and point C is 4 right of the origin.
Coordinate planes
In the 2D coordinate plane, the origin is the intersection of the x-axis and the y-axis.
The position of a point in the coordinate plane is written as an ordered pair, (x, y), which tells us the position of the point relative to the origin. To find a point in the coordinate plane, just count x squares along the x-axis from the origin, then count y squares in the y direction.
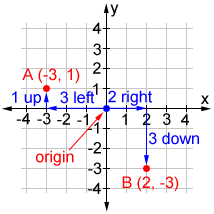
Points A (-3, 1) and B (2, -3) are graphed on the coordinate plane above. Starting from the origin, follow the steps below to find the position of the point.
- Point A: From the origin, move to the left 3 units along the x-axis to get an x-coordinate of -3 then, move up 1 unit in the direction of the y-axis to get a y-coordinate of 1.
- Point B: Form the origin, move to the right 2 units along the x-axis to get an x-coordinate of 2, then move down 3 units in the direction of the y-axis to get a y-coordinate of -3.
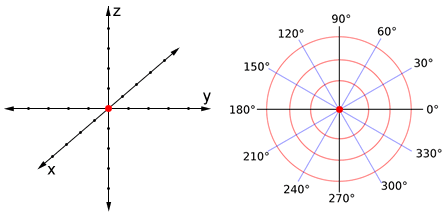
Other coordinate systems, such as a 3D coordinate system or a polar coordinate system also have an origin, as shown below. Similar to the 2D coordinate plane, the position of a point in either of these systems is also described relative to the origin.