Acute
In geometry, the term "acute" is usually used to describe a type of angle called an acute angle. It is also used to describe a type of triangle, an acute triangle, which is characterized by having only acute angles.
What is an acute angle
An acute angle is a type of angle. It is characterized by its angle measure. Some examples of acute angles in real life include the letter "V" and a slice of a pizza.
Definition of an acute angle
An acute angle is defined as any angle whose measure is between 0° and 90°. An angle with a measure of 0° would be a line, not an angle; an angle with a measure of 90° is a right angle; an angle with a measure greater than 90° is an obtuse angle.
Acute angle degree
An acute angle has a degree measure between 0° and 90°.
Complementary angles
Complementary angles are pairs of angles that sum to 90°. Since the sum of a pair of complementary angles is 90°, each angle in the pair of angles is an acute angle.
What does an acute angle look like
The following figure shows a few acute angle examples.

When identifying or measuring an acute angle, be careful about the rotation from one side of the angle to the other that produces the acute angle.

The example below shows the type of problems we can come across in geometry involving acute angles.
Example:
In the figure below, ∠MON and ∠PON are adjacent angles that are also complementary. Find the measures of ∠MON and ∠PON.

Since ∠PON and ∠MON are complementary, ∠PON + ∠MON = 90°. If we plug in the expressions for the angle measures we get,
| (2x - 3) + (x + 9) = 90 |
| 3x + 6 = 90 |
| x = 28 |
So, ∠MON = 28 + 9 = 37° and ∠PON = 2×28 - 3 = 53°.
Notice that ∠PON and ∠MON must be acute angles since their sum is equal to the measure of a right angle (90°).
Acute triangle
An acute triangle is a triangle in which each of its interior angles has a measure between 0° and 90°. Since triangle ABC below has interior angles all of which are less than 90° and sum to 180°, it is classified as an acute triangle.

Acute triangle formula
In an acute triangle, the square of two of its sides will always be larger than the third side. Given an acute triangle with sides a, b, and c:
- a2 + b2 > c2
- b2 + c2 > a2
- c2 + a2 > b2
Below is an example of the type of problem we can come across involving acute triangles.
Example:
The 3 angles formed with vertices A,B, and C of the tent below have equal measure. Can you classify the angles for triangle ABC?
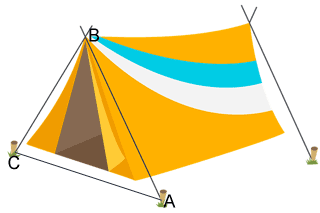
Let x represent the measure of each angle. Then,
| x + x + x = 180° |
| 3x = 180° |
| x = 60° |
So, each angle has a measure of 60° and triangle ABC is an acute triangle. The triangle can further be classified as both an equiangular triangle, since each angle has an equal measure, as well as an equilateral triangle, since each side has an equal measure.
Did you know?
Acute comes from a Latin word meaning sharp (the opposite of obtuse or dull). The vertex of an acute angle is "sharp" when compared with the vertex of an obtuse angle.
