Supplementary
Supplementary angles are two angles whose measures have a sum of 180°. Each angle is the supplement of the other.
Supplementary angles can be adjacent or nonadjacent.
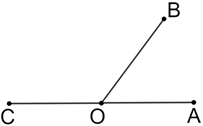
where ∠AOC is a straight angle
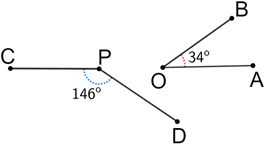
Example:
Two adjacent oblique angles make up straight angle POM below.
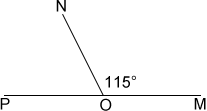
The two angles are supplementary so, we can find the measure of angle PON,
| ∠PON + 115° = 180° |
| ∠PON = 65° |
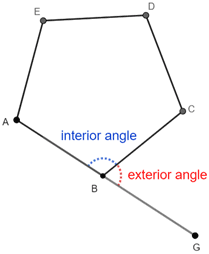
For polygons, such as a regular pentagon ABCDE below, exterior angle GBC and its interior angle ABC are supplementary since they form a straight angle ABG. This is true for all exterior angles and their interior adjacent angles in any convex polygon.
Regardless of how wide you open or close a pair of scissors, the pairs of adjacent angles formed by the scissors remain supplementary. Below, angles FCD and GCD are supplementary since they form straight angle FCG.

