Area of a rectangle
The area of a rectangle is the space contained within its perimeter. The grey space is the area of the rectangle in the diagram below.
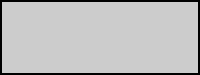
Area formula of a rectangle
The area, A, of a rectangle is the product of its length, l, and width, w.
A = l×w

Note: Sometimes, base and height are used instead of length and width.
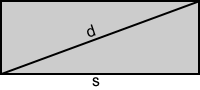
Area formula using the diagonal
If the diagonal, d, and one side, s, of the rectangle are known, the following area formula can be used:
Example:
Find the area of the rectangle below that has a diagonal of 26 and length of 24.
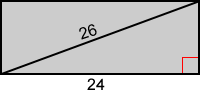
Since the area of a rectangle is a product of its length and width, we need to find the width. The diagonal of a rectangle divides it into two congruent right triangles. Using the Pythagorean theorem:
w2 + 242 = 262
w2 + 576 = 676
w2 = 100
w = 10
The area of the rectangle is:
A = l×w = 24×10 = 240
Using the diagonal and side length formula:
| A = | |
| = | |
| = | 24 × 10 |
| = | 240 |
Finding area using a grid
Another way to find the area of a rectangle is to determine how many unit squares it takes to cover its surface. Below is a unit square with length 1 cm.
A grid of unit squares can be used when determining the area of a rectangle.
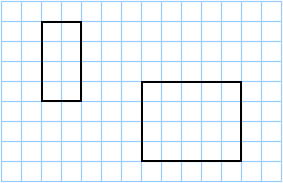
The grid above contains unit squares that have an area of 1 cm2 each. The rectangle on the left contains 8-unit squares, so it has an area of 8 cm2. The rectangle to the right contains 20-unit squares, so it has an area of 20 cm2.
