Coplanar
Objects are coplanar if they lie in the same geometric plane. Typically, we refer to points, lines, or 2D shapes as being coplanar.
Any points that lie in the Cartesian coordinate plane are coplanar. It doesn't matter what point because the coordinate plane lies in two dimensions. For a point to be non-coplanar, we would need a three-dimensional space.
What are coplanar points
Points that lie in the same geometric plane are described as being coplanar. Below are some basic facts about coplanarity of points and lines:
- Any 2 points are coplanar.
- Any 3 points are coplanar.
- If the points are collinear, there are infinitely many planes on which the points are coplanar.
- If the points are non-collinear, the plane on which the points are coplanar is unique.
- All collinear points are coplanar.
- 4 or more points are coplanar only if all 4 lie on the same unique plane.
- 2 intersecting lines are always coplanar. 3 more lines are only coplanar if all the lines lie in the same plane.
- 2 parallel lines are coplanar.
Example
The figure below shows two parallel planes, M and N, which house various points and lines that we will use to demonstrate some of the above facts.

Lines HG and FE are coplanar; neither of these lines are coplanar to line AD. If we were to form lines FG and HE, they would also be coplanar. Any 2 points selected would be coplanar; this is also true of any 3 points. However, while the 4 points H, F, E, and G are coplanar, the 4 points H, F, E, and B are not. Notice that if we select points B and F, we can construct infinitely many planes between the two points, but if we select 3 points, such as B, C, and F, they are coplanar on a unique plane.
The figure below shows another example of coplanarity in 3D spaces.
Example:
The rectangular prism below has vertices at A, B, C, D, E, F, G, and H.
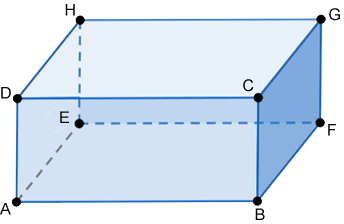
The vertices A, B, C, and D on the front face are coplanar but not collinear. This is true for each of the 6 faces that make up the prism.
Coplanar and collinear
Two points are coplanar if they lie in the same plane. They are collinear if they lie on the same line. A collinear set of points will always be coplanar. However, a coplanar set of points is not necessarily collinear. Non-coplanar and non-collinear objects are simply objects that are not coplanar and not collinear.
Example:

In the diagram above, points A, B, and C are collinear and lie in plane M, so they are collinear and coplanar (you can draw infinitely many planes containing line AB). Points A, B, C, and D lie in plane M so they are coplanar but not collinear since they do not lie on the same line.
Point F does not lie on plane M so it cannot lie on line AB. Therefore, it is neither coplanar to M nor collinear with A, B, and C.
Coplanar and non-coplanar
Coplanar objects lie in the same plane. Non-coplanar objects are those that do not lie in the same plane. 2 points will always be coplanar because they lie on the same plane in 2D space. 3 points will also always be coplanar because there is 1 unique plane on which they all lie. Once 4 or more points are involved, we cannot definitively say that they are coplanar. They are non-coplanar if even one of the points lies on a different plane.
