Diameter
The diameter of a circle is a line segment that passes through the center of the circle and has endpoints on the circle.
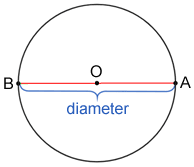
Line segment AB above is a diameter for circle O since endpoints A and B lie on the circle and line segment AB passes through center O.
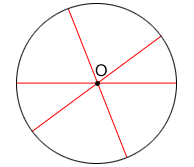
A circle contains infinitely many diameters. Three diameters are drawn for circle O below. As long as the line segment passes through the center and has its endpoints on the circle, it is a diameter.
Diameter and radii
The diameter of a circle is twice the length of the circle's radius.
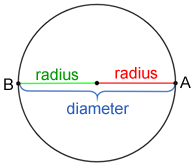
The two radii of length r, shown above for the circle, form diameter d. Since each radius of a circle has equal measure, d = 2r or .
Diameter and chords
A chord is a line segment whose endpoints are on a circle. If a chord contains the center, it is also a diameter of the circle. A diameter is longer than any chord that does not contain the center (i.e. is not a diameter).
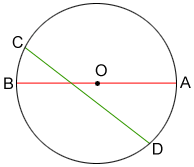
Diameter AB > chord CD for circle O above since chord CD does not contain center O.
Diameter and circumference
The circumference of a circle can be compared with its diameter.

If the circumference of a circle is straightened to make a line segment shown above, its length is a little longer than the length of 3 of the circle's diameters. The circumference of a circle is its diameter scaled by pi (written symbolically as π). This is true for any circle of any size. Pi is a mathematical constant and an irrational number, so it has an infinite number of digits, and no repeating pattern. It is approximately equal to 3.14159.
Diameter and semi-circles
An arc of a circle whose endpoints lie on the endpoints of a diameter of the circle forms a semi-circle or half-circle.
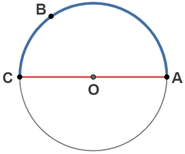
The endpoints of arc ABC for circle O shown above lie on the endpoints of diameter AB, forming a semi-circle. Additionally, a diameter divides a circle into two semi-circles, so the arc below arc ABC is also a semi-circle.
Since the semi-circle encompasses one-half of the entire circle, its circumference is one-half the circumference of the circle, or πr, where r is the radius of the circle.
Other properties and theorems
If the vertex of a right angle lies on a circle, then the points of intersection of the sides of the angle and the circle form a diameter of the circle.
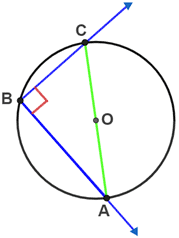
The vertex of right angle B is on circle O, shown above. The measure of an inscribed angle is one-half the measure of its intercepted arc. Since angle B is an inscribed angle and its measure is 90°, intercepted arc has a measure of 180°. Thus, the arc is a semicircle and chord AC is a diameter of circle O.
Conversely, if the vertices of a triangle are on a circle and one side of the triangle is a diameter of the circle, then the angle opposite of the diameter is a right angle and the triangle is a right triangle.
If a chord of a circle is the perpendicular bisector of another chord, the chord that is the perpendicular bisector is a diameter of the circle.
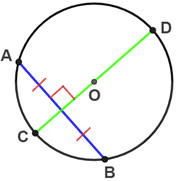
Chord CD is the perpendicular bisector of chord AB for circle O, shown above, so chord CD is a diameter of the circle.
Diameter of spheres
A chord for a sphere is a line segment whose endpoints are on the sphere. If the chord contains the center of the sphere, it is a diameter of the sphere.

Two chords, chord AB and chord CD, are drawn inside the sphere with center O, shown above. Since chord AB contains the center of the sphere, chord AB is a diameter of the sphere. A diameter of a sphere lies on a great circle of the sphere. A great circle divides a sphere into two semi-spheres (half spheres).

The semi-sphere above the great circle containing diameter AB is shown above. The semi-spheres above and below the great circle are the same size. This is true for any two semi-spheres of a sphere.
