Sphere
A sphere is a 3D geometric figure that has a round shape. All points on the surface of the sphere are an equal distance from its center.
Below are some real-life examples of spheres. A basketball, the Earth, and an orange are all examples of geometric figures that have the shape of a sphere.

Properties of a sphere
In Geometry, a sphere is defined as the set of all points in space that are equidistant from a fixed point (the center) of the sphere.
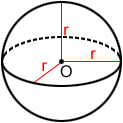
Radius
A radius, r, of a sphere is a line segment from the center of the sphere to any point on the sphere's surface. Three radii (plural for radius) are graphed for the sphere with center at point O below.
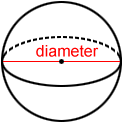
Diameter
Like a circle, a diameter of a sphere is any chord that passes through its center, as shown below.
Great circle
The intersection of a plane and a sphere containing the sphere's center creates a circle. This circle is called a great circle. A plane that intersects a sphere without going through the center will also create a circle. However, it is not a great circle, since a great circle is the largest possible circle that can be created by the intersection of a plane with a sphere. Any other circular intersection has a radius smaller than the great circle.
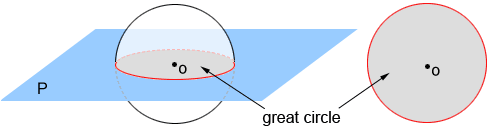
Plane P above intersects sphere O through center O creating a great circle of the sphere, shown in grey. The great circle divides the sphere into two equal hemispheres.

Three great circles in black, red, and green are shown for sphere O above. A sphere contains infinitely many great circles. Each great circle is considered a plane of symmetry since it divides the sphere into two equal parts. This means that a sphere has infinitely many planes of symmetry.
Volume of a sphere
The volume, V, of a sphere is
where r is the radius of the sphere.
Surface area of a sphere
The surface area, S, of a sphere is
S = 4πr2
where r is the radius of the sphere.
