Rhombus
A rhombus is a parallelogram in which all sides are congruent. The shape of a rhombus is also often referred to as a diamond, like the suit in a standard deck of cards.

Sides of a rhombus
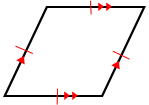
All sides of a rhombus are congruent, and its opposite sides are parallel.
Angles of a rhombus
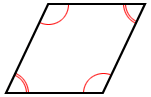
Like a parallelogram, opposite angles of a rhombus are congruent. Also, the adjacent angles of a rhombus are supplementary, meaning that each pair of adjacent angles sums to 180°, and the sum of all the interior angles equals 360°.
Diagonals of a rhombus
A rhombus can have two diagonals; the diagonals are perpendicular bisectors of each other.
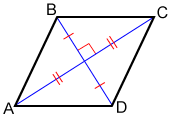
Diagonals and are perpendicular bisectors of each other for rhombus ABCD above.
The diagonals of a rhombus bisect its angles:

Diagonals and bisect the opposite angles of rhombus ABCD above.
Square
A square has four congruent sides and four right angles making it a special case of a rhombus. A rhombus is also a square when all its angles are right angles.

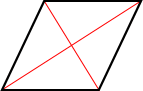
Symmetry in a rhombus
A rhombus has 2 lines of symmetry and a rotational symmetry of order 2, which means that it can be rotated in such a way that it will look the same as the original shape 2 times in 360°.
| Line of symmetry | Rotational symmetry |
|---|---|
 |
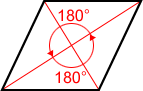 |
| Both diagonals are lines of symmetry | 180° angle of rotation about its center |
Area of a rhombus
The area of a rhombus with diagonals d1 and d2 is,
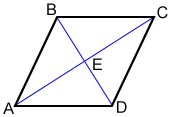
Let AC = d1 and BD = d2 for rhombus ABCD above. Rhombus ABCD can be divided into triangles ABC and ADC by diagonal AC. The area of △ABC = AC×BE where BE is the altitude of △ABC. The area of △ADC =
AC×DE where DE is the altitude of △ADC. The area of rhombus ABCE equals the sum of the areas of △ABC and △ADC.
| Area = | Area of △ABC + △ADC |
| = | |
| = | |
| = | |
| = |
If the length of base (b) and height (h) of a rhombus were given, the area of a rhombus is,
A = b·h
