Parallelogram

A parallelogram is a quadrilateral with two pairs of opposite, parallel sides. In the figure below are 4 types of parallelograms.

Sides of a parallelogram

A parallelogram has 4 sides. The opposite sides of a parallelogram are equal in length. In the figure below, side BC is equal to AD in length and side AB is equal to CD in length.

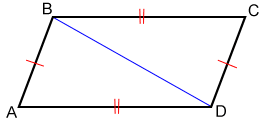
Diagonal BD cuts parallelogram ABCD into two triangles.. Since AD//BC, ∠ADB = ∠DBC. Since AB//DC, ∠ABD = ∠BDC. According to the Angle-Side-Angle (ASA) postulate, △ABD ≅ △CDB. Therefore, AB ≅ CD and AD ≅ BC.

Interior angles of a parallelogram

A parallelogram has 4 internal angles. The opposite angles of a parallelogram are equal in measure. The consecutive angles are supplementary to each other. The sum of the interior angles is 360°.

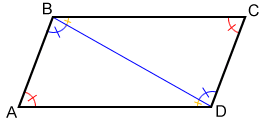
In the diagram above, diagonal BD cuts parallelogram ABCD into two triangles. Since AD//BC, ∠ADB = ∠DBC. Since AB//DC, ∠ABD = ∠BDC. Therefore

∠ABC	= ∠ABD + ∠DBC
	= ∠BDC + ∠ADB
	= ∠ADC

Similarly, it can be proven that ∠A = ∠C.

Since ∠ADB = ∠DBC and the sum of the angles of a triangle is 180°,

∠A + ∠B	= ∠A + ∠ABD + ∠DBC
	= ∠A + ∠ABD + ∠ADB
	= 180°

Therefore, ∠A and ∠ABC are supplementary.

Similarly, it can be proven that ∠B + ∠C = 180°, ∠C + ∠D = 180°, and ∠A + ∠D = 180°. Also ∠A + ∠B + ∠C + ∠D = 360°.

Diagonals of a parallelogram

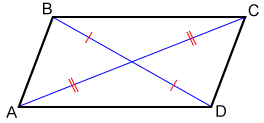
A parallelogram has two diagonals. The diagonals of a parallelogram bisect each other. In the figure below diagonals AC and BD bisect each other.

Special parallelograms

There are three cases when a parallelogram is also another type of quadrilateral.

Rhombus	Rectangle	Square
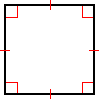Parallelogram with all sides equal in length	Parallelogram with four right angles	Parallelogram with four right angles and all four sides equal in length

Symmetry in a parallelogram

A parallelogram has rotational symmetry of order 2.

Rotating the parallelogram above 180° about point E will result in a parallelogram that is the same as the original shape.

Area of a parallelogram

The area of a parallelogram is the product of the length of its base (b) and height (h).

A = b·h

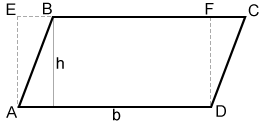
In the diagram above, △ABE ≅△DCF. Therefore the area of parallelogram ABCD is equal to the area of rectangle AEFD, or b×h.