Triangle
A triangle is a 3-sided polygon.
Triangle definition
A triangle is a closed, two-dimensional shape that has 3 sides, 3 angles, and 3 vertices. It is the polygon with the fewest sides. Since it is the simplest form of a polygon, any polygon can be constructed using two or more triangles.
Parts of a triangle
The following list describes various common parts of a triangle:
- Side - A side (or edges or leg) of a triangle is one of the three line segments that form the triangle.
- Vertex - The vertex of a triangle is a point at which two sides meet.
- Angle - An angle is formed by the intersection of 2 rays. For a triangle, an angle is formed at each vertex.
- Base - The bottom side of a triangle (any side can be the base.)
- Altitude - The perpendicular line segment formed between the vertex of a triangle and the side opposite the vertex.
- Interior angle - The angles formed inside a triangle by its vertices.
- Exterior angle - The angle formed outside a triangle by extending a side.
- Median - The line segment joining a vertex of a triangle to the midpoint of the side opposite the vertex.
Triangle notation and labeling
Various notation are used to label triangles.
Naming triangles
One way that triangles are named is by labeling their vertices using either lower case or upper case letters, as shown in the figure below:

The triangle above is named △ABC.
Naming sides
The sides of the triangle above are named using the line segments between vertices: AB, BC, and AC.
Triangle sides can also be labeled based on its opposing angle:

In the triangle above, the lower case letters are the sides and the upper case letters are their opposing angles.
Naming angles and vertices
Referencing the above triangles, an interior angle is formed at each vertex of a triangle. These angles share the same name as their vertices. Thus, the three interior angles for △ABC above are A, B, and C.
Triangle sides, angles, and congruence
The measure of a triangle's sides and angles relative to each other can be indicated using tally marks and arcs. Refer to the figure below:

The higher the number of tally marks or arcs, the larger the side or angle respectively. If there are the same number of tallies or arcs, the sides or angles involved are congruent.
If the angle is a right angle, rather than using an arc, the symbol ⌞ is used instead. The figure below shows a right triangle and the symbol denoting the 90° angle:

Types of triangles
Any triangle can classified as either acute, obtuse, or right. Triangles can be further classified as equilateral, isosceles, or scalene.
Acute triangle
An acute triangle is a triangle in which all of the interior angles measure less than 90°. The figure below shows an acute triangle example.

Obtuse triangle
An obtuse triangle is a triangle in which one of the interior angles measures between 90° and 180°. Since the sum of the interior angles of a triangle must be equal to 180°, the remaining two angles of an obtuse triangle are acute angles that sum to a value that is less than 90°. The figure below shows an obtuse triangle example.

Right triangle
A right triangle is a triangle that has one interior angle that measures 90°. The remaining two angles are acute angles. The figure below shows a right triangle example.

Equilateral triangle
An equilateral triangle is a triangle in which all the sides and interior angles have the same measure (60°). The figure below shows an equilateral triangle example.

Isosceles triangle
An isosceles triangle is a triangle that has two interior angles of equal measure and therefore two sides of equal length. The figure below shows an isosceles triangle example.

Scalene triangle
A scalene triangle is a triangle in which none of the sides and interior angles have the same measure. Below is a scalene triangle example.

Special triangles
There are a number of special right triangles that have predictable side and angle measures. Whenever we come across these triangles, we can use their known properties to more easily solve certain geometry or trigonometry problems.
30-60-90 triangle
A 30-60-90 triangle is a special type of right triangle that has angle measures of 30°, 60°, and 90°. The figure below shows the relationship between the sides of a 30-60-90 triangle.

Due to these relationships, knowing just one side length of the triangle enables us to quickly find the lengths of the other sides without needing to directly use the Pythagorean theorem.
Example
Find the other two lengths of the 30-60-90 triangle shown below.

To find side b, we use the relationship . We know that,
so solving for x yields:
Since side b = x,
Then, the final side c = 2x, so:
Regardless which side we know, we can find the other two with some algebra.
45-45-90 triangle
A 45-45-90 triangle is another type of special right triangle. A 45-45-90 triangle is an isosceles right triangle, so the two acute angles measure 45° each. The figure below shows a 45-45-90 triangle and the relationships between its sides and angles.

Due to the relationship between the sides shown in the figure above, knowing the length of either of the congruent sides allows us to find the length of the hypotenuse using algebra. Similarly, if we know the length of the hypotenuse, we can find the length of the sides.
Example
Find the lengths of the missing sides of the 45-45-90 triangle below.

Side b = 12 because it has the same measure as the known side. To find side c, we use the relationship . Since x in this case is 12, we find c by multiplying by
:
Pythagorean triangle
A Pythagorean triangle is a special right triangle made up of Pythagorean triples. A Pythagorean triple is a set of three integers that represent the sides of a right triangle. In other words, three integers a, b, and c are a Pythagorean triple if they satisfy the Pythagorean theorem:
a2 + b2 = c2
Then, given that (a, b, and c) is a Pythagorean triple, we can also determine that any multiple of a, b and c, (ka, kb, kc) will be a Pythagorean triple.
Example
Determine whether the sides of the following right triangle form a Pythagorean triple. If so, sketch a similar triangle that represents the same Pythagorean triple.

To test whether a (3, 4, 5) is a Pythagorean triple, we just plug it into the Pythagorean theorem to see if the left side of the equation matches the right:
Since 9 + 16 = 25, (3, 4, 5) is a Pythagorean triple. We can then find a similar triangle that represents the same Pythagorean triple by multiplying by any integer, such as 2, to find the Pythagorean triple (6, 8, 10):

(3, 4, 5) is just one Pythagorean triple. The table below shows the 16 Pythagorean triples up to 100.
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Properties of triangles
The list below describes several triangle properties that are applicable to all types of triangles.
- A triangle is a polygon with 3 sides, 3 angles, 3 vertices.
- The lengths of the sides of a triangle correspond to the measures of their angles; the larger the angle, the larger the side; the smaller the angle, the smaller the side. The longest side of a triangle is opposite the angle with the largest measure and the shortest side of the triangle is opposite the smallest angle.
- Angle sum property - The sum of the interior angles of a triangle is always equal to 180°. The sum of the exterior angles of a triangle is always equal to 360°
- Triangle inequality - The sum of the lengths of two sides of a triangle is always larger than the length of the third side; the difference between the lengths of any two sides is less than the length of the third side.
- Exterior angle theorem - The measure of an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles of the triangle.
- Congruent - Two triangles are congruent if all of their corresponding sides and angles are equal.
- Similar - Two triangles are similar if all their corresponding angles are equal and their corresponding sides have the same ratio. In other words, the shape of the triangle is identical, but the size of the triangles are different.
- The sum of consecutive interior and exterior angles of a triangle is supplementary (180°).
Angle sum property proof
Using properties of parallel lines and alternate interior angles, we can show the sum of the interior angles for a triangle is 180°.
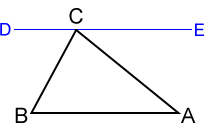
- For △ABC shown above, let line DE, containing vertex C, be parallel to side AB. Since ∠DCE is a straight angle, ∠ECA + ∠DCB + ∠BCA = 180°.
- Also, since DE is parallel to AB, this forms two sets of congruent alternate interior angles such that ∠ECA≅∠A and ∠DCB≅∠B.
- Substituting angles A and B into our previous equation, ∠A + ∠B + ∠BCA = 180°, where ∠BCA = ∠C.
Exterior angle theorem proof
For a triangle, an exterior angle is an angle formed by one side of the triangle and a line extended from another of its sides. The measure of an exterior angle of a triangle equals the sum of its two remote interior angles.
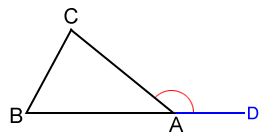
For △ABC shown above, ∠CAD is the exterior angle for ∠A and ∠B and ∠C are the two remote interior angles. We know that ∠CAB + ∠B + ∠C = 180°. Also, ∠CAB and ∠CAD form a straight angle, so ∠CAB + ∠CAD = 180°. Since both sums equal 180°:
∠CAB + ∠CAD = ∠CAB + ∠B + ∠C
∠CAD = ∠B + ∠C
The same can be shown for any exterior angle of any triangle.
Comparing sides and angles
A triangle can only be formed when the sum of any two sides of the triangle is greater than its third side; if the sum of the two sides is shorter than the third, they will never meet to form a polygon; if the sum of the two sides is equal to the third, they will overlap and form a line.
Example:
The sides of △ABC are a = 4, b = 6, and c = 9. Can a triangle be formed with the given sides?
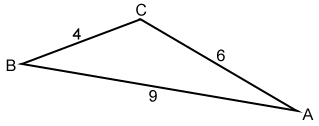
Since 4 + 6 > 9, 4 + 9 > 6, and 6 + 9 > 4 we can form △ABC. This only tells us that a triangle can be formed by the three given sides. It does not classify the triangle.
Triangle formulas
Below are some formulas for calculating the perimeter and area of a triangle, as well as for finding the angle and side measures of a triangle.
Perimeter of a triangle
The perimeter of a triangle is the sum of the lengths of its 3 sides. Given sides a, b, and c of a triangle, the perimeter P is computed as:
P = a + b + c
Area of a triangle
The area of a triangle is found using the formula,
where b is the base of the triangle and h is the height of the triangle. Any side of the triangle can be used as the base; the height is the perpendicular distance drawn from the vertex opposite the chosen base. Refer to the figure below.

The above two triangles are the same triangle in different orientations. The heights relative to the selected base are shown. Regardless which base is selected, the area of the triangle will be the same.
Heron's formula
Heron's formula is another formula for computing the area of a triangle. Heron's formula is as follows,
where a, b, and c are the sides of the triangle and s is its semiperimeter:
Converse Pythagorean theorem
The converse Pythagorean theorem helps us identify whether a triangle is acute, right, or obtuse. The Pythagorean theorem states that for a right triangle with sides a, b, and c,
a2 + b2 = c2
The converse of the Pythagorean theorem states that for any triangle with sides a, b, and c, if a2 + b2 = c2, then the triangle is a right triangle and the angle measure between a and b is 90°.
How to tell if a triangle is acute, obtuse, or right
To tell whether a triangle is acute, obtuse, or right, we can use the converse of the Pythagorean theorem as follows:
- If a2 + b2 > c2, the triangle is an acute triangle.
- If a2 + b2 = c2, the triangle is a right triangle.
- If a2 + b2 < c2, the triangle is an obtuse triangle.
Example
Determine whether the triangle below is acute, right, or obtuse. Note that the triangle is intentionally not drawn to scale.

Let a = 12, b = 23, and c = 27. Then:
Since 673 < 729, the triangle is obtuse. The actual triangle to scale looks like this:

Note that the angle measures are approximate and rounded to 3 digits, so they will not perfectly sum to 180°.
Law of sines
The law of sines, also referred to as the sine rule, is a formula that is useful for finding the sides and angles of a triangle. The law of sines works for any triangle, unlike some of the rules and special triangles described in the sections above. The law of sines is as follows,
where a, b, and c are the sides of the triangle and A, B, and C are their corresponding angles, as shown in the triangle below:

Depending on the known information, the law of sines can be used to find the missing angles or sides of a triangle. All we need is a minimum of 3 values (either angles or sides) of the triangle.
Example
Find the missing sides and angles of the following triangle using the law of sines.

In the above triangle, we know the measure of one side and 2 angles. The angle 26.241° corresponds to the side with length 12, and the 57.936° angle corresponds to side b, which we can find using the law of sines:
Then, since we know that the sum of the angles of a triangle must equal 180°, we can find angle C by subtracting the known angles from 180°:
180° - 57.936° - 26.241° = 95.823°
Then, to find the final side, we can apply the law of sines again with either of the sides and angles to find that the final side c = 27.
The law of sines is useful because it applies to any triangle. There are simpler ways to find the lengths and angles of other types of triangles such as right triangles, but those simpler methods only work in very specific cases. Understanding the law of sines allows us to find the sides and angles of any triangle given sufficient information.
Law of sines ambiguous case
Although the law of sines is a powerful tool, in the case where two sides and an angle not between the two sides are known (SSA), there are three possible outcomes:
- No triangle exists. This case occurs if A is an acute angle and a < h, or if A is obtuse and a ≤ b.
- Two triangles exist. This case occurs when the length of side a is greater than the height of the triangle, but less than side b: h < a < b.
- Exactly one triangle exists. This case occurs if A is acute and a = h, A is acute and a > b > h, or A is obtuse and a > b.
Law of cosines
The law of cosines, also referred to as the cosine rule, is a formula we can use in certain cases to find the angles and sides of a triangle. The law of cosines is as follows:
The law of cosines can be used to find,
- the third side of a triangle given two sides and the angle between them.
- the angles of a triangle given all three sides.
Law of cosines for angles
The law of cosines can be rearranged to the following forms, which may be more straightforward for certain cases:
Example
Find the missing sides and angles of the following triangle using the law of cosines.

Let a = 9, b = 13, and C = 42°. Plugging these into the law of cosines, we can solve for
Thus, side c = 8.724.
To find the remaining two angles, A and B, we can use the rearranged forms of the law of cosines:
Thus angle A = 43.655°. Angle B can be found in the same manner:
Note that we could have also found B by simply subtracting A and C from 180°, since the sum of the interior angles of all triangles must equal 180°.
Congruent triangles
Two triangles are congruent if their corresponding sides and angles are equal. There are 5 congruence criteria that make it relatively simple to determine whether two given triangles are congruent. Two triangles are congruent:
- Side-side-side (SSS) - when all three pairs of corresponding sides of two triangles are congruent.
- Side-angle-side (SAS) - when two pairs of corresponding sides as well as the angle between them are congruent
- Angle-side-angle (ASA) - when two pairs of corresponding angles as well as the sides between them are congruent.
- Angle-angle-side (AAS) - when two pairs of corresponding angles as well as a pair of sides not between the angles are congruent.
- Hypotenuse-leg (HL) - when the hypotenuses of a right triangle and a pair of its corresponding sides are congruent.









