Area of a triangle
The area of a triangle is the region that is bounded by its three sides.
The area of a triangle can be found using a number of different methods.
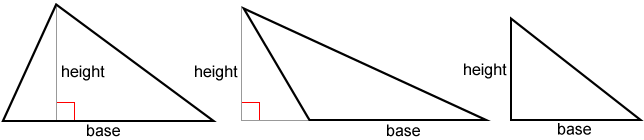
Using base and height
Given base b and height h for a triangle, the area of the triangle is:
The height of a triangle is perpendicular to its base. It can be either inside, outside, or on the side as shown in the figure below.
The formula above can be proven using the area of a parallelogram. The formula for the area of a parallelogram is base × height, written as Area = b × h. A diagonal of a parallelogram divides it into two congruent triangles as shown in parallelogram ABCD below.
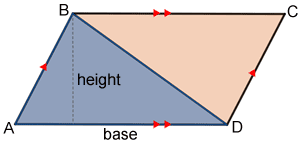
Since △ABC≅△CBD, the area of △ABC is half the area of the parallelogram. Therefore, the area of △ABC=. Similarly, the area of △CBD=
.
Using its sides
If the three sides of a triangle are given, the area can be found using Heron's formula.
where a, b, and c are the lengths of the three sides of the triangle, the semi-perimeter, s, is .
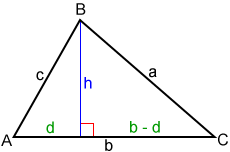
One way to prove Heron's formula is by using the Pythagorean Theorem. In the figure above, we have d2 + h2 = c2 and (b - d)2 + h2 = a2. Subtracting these we get 2bd = b2 + c2 - a2. So,
Since h2 = c2 - d2
| h2 = | |
| = | |
| = | |
| = | |
| = | |
| = |
| Area = | |
| = | |
| = |
Using trigonometry
If two sides and an included angle are given for a triangle, we can find its area using the following formulas:
where A, B, and C are the 3 angles of the triangle and a, b, and c are the lengths of the 3 sides opposite the 3 angles.
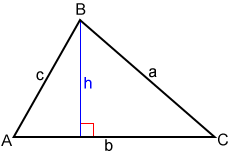
For the triangle shown above with base b, height h, sides a, and angle C given, we can use the sine function to get and find that h = a × sin(C).
Using Area = .
Example:
For △ABC, a = 7, b = 4, and ∠C=40°. Find the area of the triangle.
Since we are given two sides and an included angle we can use the following formula to get,
| Area = | |
| = | 14 × 0.6428 |
| = | 8.9992 |
