Similar triangles
Similar triangles are triangles whose corresponding angles are congruent. In mathematics, the symbol "~" is used to convey that two or more objects are similar.
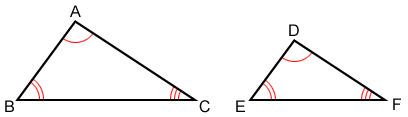
Similarity theorems
There are a number of different ways to find out if two triangles are similar. The following are a few of the most common.
Angle-Angle (AA) theorem
If two angles in one triangle are congruent to two angles of another triangle, the triangles are similar.
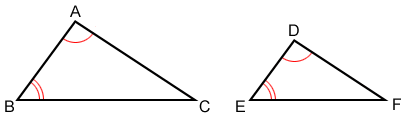
In the figure above, if ∠A≅∠D , ∠B≅∠E then, △ABC~△DEF.
Example:
Show that △EFI~△EGH given that //.
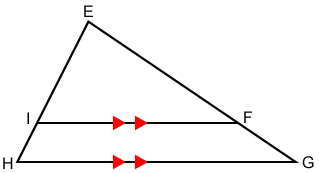
Since //, ∠EFI≅∠G and ∠EIF≅∠H. Therefore, △EFI~△EGH by the AA similarity theorem.
Side-Side-Side (SSS) theorem
Two triangles are similar if the lengths of their corresponding sides are proportional.
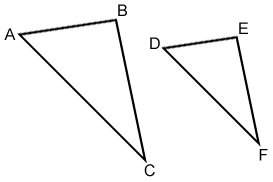
In the figure above, if , then △ABC~△DEF. Note that the corresponding sides do not have to be equal in length.
Side-Angle-Side (SAS) theorem
Two triangles are similar if one of their angles is congruent and the corresponding sides of the congruent angle are proportional in length.

In the figure above, if , and △IEF and △HEG share the same angle, ∠E, then, △IEF~△HEG.
