Pentagram
A pentagram is a polygon in the shape of a five-pointed star. Below are two different types of pentagrams.

The pentagram is part of the national flags of many countries. The following are a few examples.

Regular pentagram
A regular pentagram consists of 5 congruent isosceles triangles forming the 5 points, and a regular pentagon in its center.
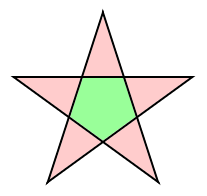
Irregular pentagrams
The triangles forming the 5 points of an irregular pentagram are not all congruent. It follows that the pentagon in the center of an irregular pentagram is an irregular pentagon.

Construct a regular pentagram
A regular pentagram can be constructed by drawing the 5 diagonals of a regular pentagon.

Two distinct diagonals can be drawn from any vertex of a regular pentagon. Drawing diagonals from all the vertices, as shown in the regular pentagon above, forms a regular pentagram.
You can also extend the sides of a regular pentagon to form a pentagram.
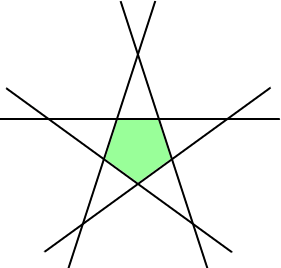
The five points of intersection formed by extending each side of the regular pentagon shown above form the five points of a regular pentagram.
Angle measures of a regular pentagram
The angles formed at each of the five points of a regular pentagram have equal measures of 36°.
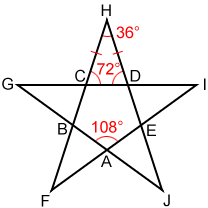
For regular pentagon ABCDE, shown above, each interior angle has a measure of 108°. Angle BCD = 108°, so its supplement, angle HCD = 72°. Since the five triangles forming pentagram FGHIJ are isosceles, their base angles are congruent, so angle HDC = 72°.
Also, the sum of the interior angles of a triangle is 180°, so angle H = 180° - (72° + 72°) = 36°. The same is true for angles F, G, and I, which also have measures of 36°.
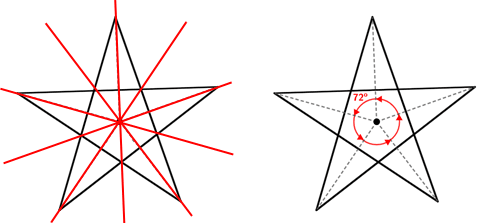
Symmetry in a regular pentagram
A regular pentagram has 5 lines of symmetry and a rotational symmetry of order 5, which means that it can be rotated in such a way that it will look the same as the original shape 5 times in 360°.